Molte persone iniziano ad utilizzare il PC semplicemente smanettando con i più comuni pacchetti applicativi (per es. quelli di automazione d'ufficio come Microsoft® Word® o Excel®) e tralasciano i concetti base che invece sono molto utili, se non indispensabili, per acquisire una sufficiente padronanza di questo aspetto del mondo informatico.
Infatti l'utilizzo del PC spesso si spinge più in là del semplice utilizzo atto all'immissione dei dati (uso ufficio) o alla navigazione in internet (uso domestico). Ed anche se l'utilizzo del PC è posto a livelli elementari, la conoscenza di alcuni concetti di base non può far altro che aprire in misura esponenziale la capacità di intuire e di padroneggiare le innumerevoli possibà che anche il semplice utilizzo del personal computer ci offre.
Quante volte incontriamo persone che, pur avendo già una piccola padronanza e conoscenza di alcuni pacchetti applicativi, non sanno dell'esistenza di una memoria chiamata "Appunti", di una tecnologia chiamata "O.L.E.", di quale sia il senso del "percorso" di un file e di molte altre cose dell'ambiente operativo Microsoft® Windows® (giusto per fare un esempio).
Ma l'oscurità delle nozioni base si spinge anche a monte del Sistema Operativo: sono poche anche le conoscenze di cosa sia il bit ed il byte, il codice ASCII, di quane pagine di testo possano "entrare" in un floppy disk, di come vengono memorizzate le immagini e i suoni sui dischi... ecc. ecc.
Iniziamo quindi la discussione parlando di come le informazioni vengono memorizzate sul computer.
Le informazioni vengono memorizzate nelle memorie, siano esse fisse o volatili, in modo digitale.
Digitale vuol dire sotto forma di digit ovvero numeri.
In pratica i numeri utilizzati sono solo due e cioè 0 e 1 perché il linguaggio attuale dei computer è un linguaggio binario, cioè un linguaggio comunicativo composto da due soli caratteri.
Un linguaggio binario (analogico) è, per esempio, l'alfabeto Morse, chi non lo conosce almeno per sentito dire? Due soli caratteri: punto e linea, ma se si comunica con i fari alogeni i due segnali del linguaggio morse diventano un "lampo di luce" corto e un "lampo di luce" più lungo. Se si comunica con il telegrafo i due segnali diventano un "beep acustico" corto ed un un "beep acustico" più lungo.
Questo per far capire che, nel linguaggio binario informatico, è vero che si utilizzano i due caratteri numerici "0" e "1", ma è altrettanto vero che questi sono caratteri abbinati alla rappresentazione logica di tale linguaggio; dal punto di vista fisico, i due caratteri possono assumere altre identità.
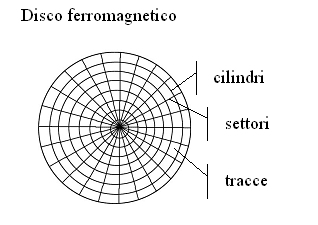
Come abbiamo detto prima, le informazioni vengono scritte sulle memorie e, di sicuro, su tali memorie non verrà mai scritto nè il carattere "1" e nemmeno il carattere "0". Prendiamo ad esempio una memoria tipica del PC: il disco fisso. Il disco fisso è composto, tra le altre parti meccaniche ed elettroniche, da un vero e proprio disco di materiale ferromagnetico. Le informazioni vengono memorizzate proprio sulla superficie di questo disco ferromagnetico. Per semplificare, possiamo dire che la superficie del disco viene suddivisa in tantissime porzioni ed ogniuna di queste può essere magnetizzata oppure non magnetizzata: ed ecco che lo stato fisico della piccola porzione del disco è in grado di rappresentare lo stato, a livello logico, del carattere "0" oppure "1".
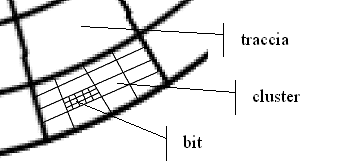
Le piccolissime frazioni di disco ferromagnetico in cui vengono memorizzati gli "0" e gli "1" (magnetizzandole oppure no) vengono chiamte bit (dall'inglese: che vuol dire una parte piccolissima che non è possibile frazionare ulteriormente - ma vuole anche dire Binary Digit) e si trovano all'interno dei cluster (o gruppi, grappoli, blocchi), che sono all'interno delle tracce che sono dovute all'intersezione tra settori e cilindri, come si vede nelle figure...
Ricapitolando: i dati vengono scritti nelle varie memorie modificando lo stato fisico (magnetizzandola o non magnetizzandola) di una piccolissima frazione della memoria stessa detta bit.
La rappresentazione logica dello stato fisico del bit viene delegata ai due caratteri numerici "0" e "1". In questo modo è possibile scrivere (e leggere) le informazioni sui vari supporti informatici digitali, utilizzando, appunto, un linguaggio binario digitale.
Per capire come le informazioni vengono scritte sui vari supporti, per capire come e quanto spazio occupano i vari
testi, le immagini, i suoni, i video ed i vari documenti multimediali, occorre capire come funziona il linguaggio binario digitale in ambito informatico.
Per esempio: come è possibile memorizzare la parola (espressa in lingua italiana) "ciao" in un supporto di memoria del nostro computer utilizzando però il linguaggio binario digitale? Ossia come possiamo tradurre una semplice parola come "ciao" in una sfilza di "0" e di "1"? Semplice: basta capire il bit ed il byte!
Supponiamo di avere una scatola non frazionabile. Possiamo quindi paragonare questa scatola al bit del nostro disco sopra descritto. Supponiamo di poter inserire in questa scatola solo due oggetti: il primo che rappresenta il numero "1" ed il secondo che rappresenta il numero "0". Supponiamo altresì che al numero "1" sia abbinata la parola "vero" oppure "sì" ed al numero "0" sia abbinata la parola "falso" oppure "no". Continuiamo a supporre che qualcuno ci faccia una domanda (per esempio: "Sei maggiorenne?") e di dover rispondere utilizzando la scatola (il bit)... facile: se nella scatola metto lo zero il mio interlocutore, quando aprirà la scatola, capirà che non sono maggiorenne; se invece metterò l'uno, capirà che lo sono.
Ma se la domanda fosse: "Come ti chiami?"
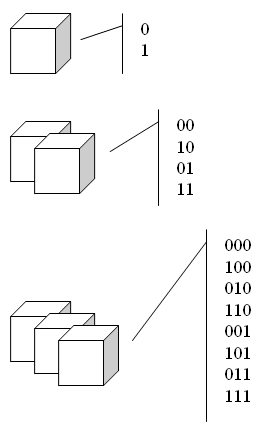
Appare chiaro che utilizzare una sola scatola per rispondere all'ultima domanda non è sufficiente.
Occorre utilizzare una serie di scatole.
Ognuna di queste scatole potrà contenere l'oggetto binario abbinato al simbolo "0" oppure "1", ma dato che le scatole sono in serie, avremo una serie di oggetti che, presi singolarmente, potranno solo rappresentare una singola informazione tra un totale di due (per es. "vero" o "falso" - "sì" o "no"), ma presi insieme, nella loro serie, possono rappresentare una singola unformazione tra un totale di molte (come un nome di persona tra un gruppo di 8 nomi di persona)... basta decidere prima una codifica.
Da questa figura, si capisce che utilizzando una sola scatola possiamo esternare 1 tra 2 soli valori ("0" o "1").
Utilizzare 2
scatole vuole invece dire poter comunicare 1 informazione su 4 ("00", "01", "10", "11").
Con 3 scatole posso addirittura esprimere 1 valore su 8 ("000", "010", "100", "110", "001", "011", "101", "111").
Ora, se abbiniamo un nome di persona ad ognuno deigli otto valori (ed il nostro nome è tra questi 8... il gioco è fatto!)... Esempio: "000"="Carlo", "010"="Marisa", "100"="Antonino", "110"="Veronica", "001"="Lorella", "011"="Sebastiano", "101"="Salvatore", "111"="Elvira".
Se il supposto interlocutore mi chiede "come ti chiami?", io darò a lui tre scatole: la prima conterrà l'oggetto che rappresenta il carattere "1", la seconda conterrà l'oggetto che rappresenta il carattere "0" così come la terza. Il mio interlocutore leggerà, una volta aperte le tre scatole in sequenza, il codice "100" che secondo la nostra codifica, vista prima, vuol dire "Antonino", il mio nome.
Ma se, anziché abbinare un nome di persona alla serie di bit (di scatole) abbinassi una lettera dell'alfabeto? Con 1 bit posso codificare informazioni (2^1) per poi esternarne 1, con 2 bit posso codificare 4 informazioni (2^2), con 3 bit posso codificare 8 informazioni (2^3), con 4 bit posso codificare 16 informazioni (2^4), con 5 bit posso codificare 32 informazioni (2^5), con 6 bit posso codificare 64 informazioni (2^6), con 7 bit posso codificare 128 informazioni (2^7), con 8 bit posso codificare 256 informazioni (2^8) per poi comunicarne sempre una.
I caratteri del nostro alfabeto (sia in maiuscolo che in minuscolo), più i caratteri di punteggiatura, più i caratteri numerici, più le lettere accentate (sia in maiuscolo che in minuscolo), più altri caratteri tipici di altre lingue europee come per es "Ä", "Ç", "Ñ", più altri detti semigrafici, possono essere codificati utilizzando 8 bit perché in 8 bit abbiamo la possibilità di ottenere una serie di 256 informazioni diverse... cioè tutti i caratteri dell'alfabeto ed oltre.
Questa serie di 8 bit si chiama byte ed i caratteri dell'alfabeto sono racchiusi in una codifica chiamata codice ASCII esteso.
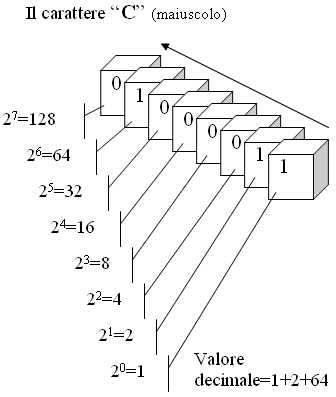
Per concludere facciamo un esempio: la stringa di testo "Ciao a tutti." verrà tradotta in linguaggio binario in "01000011 01101001 01100001 01101111 00100000 01100001 00100000 01110100 01110101 01110100 01110100 01101001 00101110" (sono occorsi 104 bit cioè 13 byte, uno per carattere, comprese spaziature e punteggiature) poiché il carattere "C" maiuscolo è codificato, secondo la tabella del codice ASCII, nella sequenza "01000011" in decimale "67" ovvero il 67º ccarattere codificato su 256, e via di seguito per gli altri caratteri.
Per ultimo ricordiamo che la sequenza del contenuto degli 8 bit (byte) va letta da destra a sinistra, per cui il primo bit a destra che in questo esempio contiene il valore "1", corrisponde al valore decimale 1, il secondo bit che contiene il valore "1", corrisponde al valore decimale 2, dal terzo al sesto bit il valore è "0", quindi anche il corrispettivo decimale è 0, il settimo bit contiene 1 quindi il corrispettivo valore decimale è 64, l'ultimo bit contiene e vale 0. Il totale fa 1+2+64= 67. Il valore decimale del codice ASCII corrispondente al carattere "C" maiuscolo vale 67.
Abbiamo capito, che il testo ASCII, quando viene memorizzato su una memoria informatica (per esempio un disco fisso) occupa tanti byte quanti sono i caratteri che compongono il testo stesso, comprese spaziature e punteggiature.
Ma se parliamo di testo ASCII, va da sè che esistono altre tipologie di testi. In effetti esistono due grandi categorie: il testo formattato e il testo non formattato.
Il testo ASCII non può essere formattato. Formattare un testo vuol dire (lo dice la parola) dare un formato al testo, in questo caso si intende un formato estetico (non fisico o logico come nel caso della formattazione di un disco).
Formattiamo un testo (o porzione di testo) ogni volta che modifichiamo, ad esempio, il colore o la dimensione del carattere, l'allineamento orizzontale o i rientri del paragrafo, le dimensioni dei margini della pagina. Quello che cambia, oltre all'estetica più accattivante, in un testo formattato (rispetto ad un testo ASCII), è il peso, ovvero la quantità di byte necessari per la sua scrittura sulla memoria (o sul disco).
Questo è facile da comprendere dato che, a differenza del testo non formattato che occupa in memoria un singolo byte per ogni carattere, il testo formattato ha bisogno di molti altri byte per la memorizzazione delle informazioni relative alla formattazione dei caratteri, dei paragrafi, delle pagine e di molti altri parametri (relativi alla formattazione e non solo).
Per verificare quanto detto, basta fare un piccolo esperimento: proviamo a scrivere un piccolo testo, per es: "Testi foramttati e testi non formattati, due mondi dello stesso pianeta..." e proviamo a memorizzarlo sia come testo non formattato (ASCII), sia come testo formattato. Per fare questo occorre utilizzare due programmi (software) diversi, tutti e due devono essere programmi detti "elaboratori di testo" ma con caratteristiche diverse. A questo scopo utilizziamo il programma Blocconote® e Word®, entrambi di Microsoft®. Il primo è un elaboratore di testo ASCII, il secondo un pacchetto applicativo per l'automazione professionale di testi (quindi anche adatto per la semplice formattazione del testo).
Memorizziamo i due file di testo nel nostro disco dando ad ognuno di loro i seguenti nomi: "testodiprova.txt" al primo (non formattato) e "testodiprova.doc" al secondo (formattato).
Ora non resta che controllare, con l'ausilio di un altro programma (Esplora Risorse - integrato nell'ambiente Windows® di Microsoft®), quanto spazio occupano (quanto pesano) effettivamente i due files (i due documenti di testo) nel nostro disco fisso.
Con Esplora Risorse (o Risorse del Computer), è possibile "vedere" tutti i files e le cartelle nei dischi (virtuali e non) del nostro PC.
Cliccando con il pulsante destro del mouse sopra il file, oggetto del nostro studio, è possibile scegliere tra le voci del menù contestuale che ne consegue, noi scegliamo la voce "Proprietà".
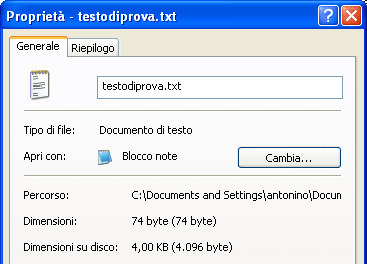
Come si vede dalle figure, il file "testodiprova.txt" pesa 74 byte (anche se sul disco occupa 4.096 byte per via del File System). I 74 byte della dimensione reale del file, corrispondono ai 74 caratteri del testo.
Infatti il testo che abbiamo scritto ("Testi foramttati e testi non formattati, due mondi dello stesso pianeta...") conta 74 caratteri, compreso le spaziature e le punteggiature.
Il fatto che lo spazio effettivamente occupato sul disco sia diverso dalle dimensioni reali del file, dipende dal File System utilizzato dal sistema operativo in uso sul PC che stiamo utilizzando. In questo caso il File System usato dal sistema operativo in uso (Microsoft® Windows®) è detto NTFS e permette Cluster minimi di 4.096 byte.
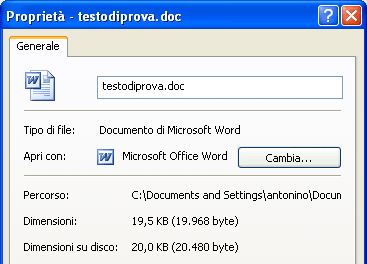
Tornando al nostro discorso, possimo vedere che, per ciò che riguarda il file relativo al testo formattato "testodiprova.doc" il peso reale è 19.968 byte: davvero molto di più dei 74 byte relativi ai 74 caratteri del testo scritto nel documento.
In pratica, come detto prima, il testo formattato deve memorizzare, oltre ai puri caratteri del testo stesso, anche tutte le informazioni relative alla formattazione estetica del documento ed è anche per ciò che pesa di più. Dato che per il testo formattato abbiamo utilizzato Word®, che è un pacchetto applicativo professionale, esso memorizza, oltre alle informazioni della formattazione estetica, anche le informazioni relative alla automazione del testo (una automazione è, per esempio, la numerazione automatica delle pagine), e, per questo, pesa ancora di più.
Le informazioni relative alla formattazione ed alla automazione del testo, incidono sul peso del file anche quando il documento, come nel nostro caso, è composto da pochissimi caratteri, con pochissima formattazione e nessuna automazione. Questa volta, la dimensione su disco, occupata dal file di testo formattato, è di 20.480 byte ovvero 5 cluster, o blocchi, ognuno da 4.096 byte dato che, come detto prima, il File System in uso, in questo caso è NTFS.
Vediamo adesso come vengono memorizzati i dati che rappresentano le immagini. Ovvero, come viene tradotta in linguaggio binario un'immagine. Quale è la tabella che permette la conversione del dato analogico in digitale.
Per esempio: quanti e quali "0" e "1" servono per "inserire" una fotografia in una memoria informatica.
Per rendere la lezione il più comprensibile possibile, tratteremo il caso di una immagine RASTER (o BITMAP, cioè mappa di bit, insieme di puntini).

Per tradurre in digitale una immagine bitmap, per prima cosa, occorre scomporre l'immagine in tante piccole particelle. Le particelle vengono chiamate "pixel" (oppure "punti" oppure "bit") e sono il frutto della divisione (intersezione) della immagine stessa in tante parti (righe) orizzontali ed altre parti (colonne) verticali.
Da notare che i pixel sono dei quadrati perfetti e non dei cerchietti o dei rettangoli, anche se, siccome sono in genere molto piccoli, senza un opportuno ingrandimento, sembrano dei puntini.

Per esempio, possiamo considerare questa immagine che rappresenta il Duomo di Chivasso (TO). Per capire cosa e dove sono i pixel che rappresentano i tantissimi puntini (quadratini) di cui è composta l'immagine stessa, abbiamo ingrandito più volte un particolare del campanile che vediamo nei cerchiolini rossi.
Alla fine l'immagine è abbastanza ingrandita e si vedono benissimo i "quadratini", frutto dell'intersezione tra le righe e le colonne menzionate prima.

Ognuno di questi piccolissimi quadratini (nella quarta figura li viediamo grandi perché abbiamo "zoommato" l'immagine) rappresentano la parte più piccola e non maggiormente frazionalbile dell'immagine, da qui il nome pixel, acronimo in lingua anglosassone di picture element.
Ogni pixel è "pieno di un colore", ed è proprio il codice del colore di ogni pixel che sarà memorizzato nella memoria grazie ad una apposita tabella di conversione.
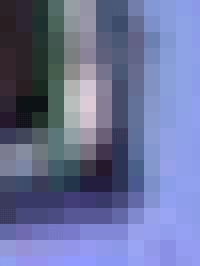
C'è quindi una analogia con quanto detto per il testo: ogni carattere del testo (elemento unitario del testo) viene memorizzato grazie ad una tabella di conversione (tabella ASCII), ogni pixel dell'immagine (meglio dire il colore di ogni pixel) viene memorizzato utilizzando una tabella di conversione (tabella RGB).
Ricordiamo che il colore è dovuto alla riflessione della luce sulle superfici, infatti, in scarsità di luce i colori tendono a sparire e, se l'assenza di luce è totale, non vediamo più nulla oppure vediamo tutto nero, ovvero, ogni oggetto (ed anche l'osservatore) viene immerso nel buio assoluto.
In presenza di luce, lo spettro dei colori che l'occhio umano riesce a percepire va dall'ultravioletto all'infrarosso passando attraverso i tre colori primari (rosso, verde e blu) e i tre secondari (ciano magenta e giallo, ottenuti dalla fusione dei colori primari, per es: luce rossa + verde = luce gialla; luce rossa + blu = luce magenta; luce blu + verde = luce ciano), che, mischiandosi tra di loro, producono una molteciplità quasi infinita di gradazioni e sfumature diverse.

La tabella di conversione RGB è molto utilizzata per le immagini in "True color" (colore vero) ovvero quelle immagini formate da milioni e milioni di pixel colorati con tutte le sfumature di colore che i nostri occhi possono percepire: circa 12/13 milioni di sfumature di colore diverse. Ma torniamo al bit e al byte.
Una serie di 8 bit permette 256 combinazioni diverse (2^8), quindi, se i colori di una immagine fossero al massimo 256, potremmo utilizzare una tabella di conversione utilizzando un singolo byte per ogni colore (quindi per ogni pixel dell'immagine).
Dato che le possibili combinazioni, cioè i possibili colori (che ogni pixel può ospitare) sono, nelle immagini True color, molto più di 256, dobbiamo utilizzare più byte per organizzare una tabella di conversione. Utilizziamo perciò un byte per ognuno dei tre colori primari RGB (Red, Green e Blue; tradotto in italiano: rosso, verde e blu). Tre byte vuol dire una serie di 24 bit (2^24) cioè 16.777.216 combinazioni per "tutte le sfumature" di colore visibili dai nostri occhi.
In pratica, abbiamo la possibilità, con la tabella RGB, di mescolare 256 gradazioni diverse di luce rossa con 256 gradazioni diverse di luce verde e con 256 gradazioni diverse di luce blu.
La gradazione massima corrisponde al massimo della luce abbinata al colore, la gradazione minima corrisponde al buio totale (totale mancanza di luce).
Se tutti e tre i canali sono al massimo della loro luce otteniamo il bianco, se tutti e tre sono a zero, avremo il buio cioè il nero.
Questo metodo si presta per visualizzare le immagini sui monitor o sulle TV.
Per esempio, se volessimo rappresentare il colore rosso secondo la tabella di conversione RGB, dovremmo dare 256 frazioni di luce (luce massima) al colore rosso, 0 frazioni di luce (luce assente) al colore verde e 0 frazioni di luce (luce assente) al colore blu.
Potremmo anche dire: il colore rosso è illuminato al massimo, mentre gli altri due non lo sono affatto, perciò non si vedono.
Il codice del colore rosso sarà quindi (in decimale, utilizzando tre bit, tre cifre numeriche per colore) "256-000-000". Se vogliamo tradurre il codice decimale in binario ecco il risultato: "11111111-00000000-00000000". Spesso, in informatica, si usa il valore esadecimale; ecco il codice esadecimale (utilizzando 2 bit, 2 caratteri esadecimali per colore) del rosso: "FF0000"
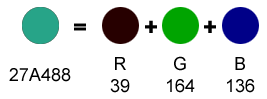
Altro esempio: se illuminiamo il colore rosso per 39/255esimi (cioè pochissimo, infatti vediamo il secondo cerchio quasi nero), il colore verde per 164/255esimi ed il colore blu per 136/255esimi, il risultato sarà il colore che vediamo nel primo cerchio.
Il codice decimale del colore del primo cerchio sarà: "039-164-136", il codice esadecimale sarà: "27A488", ed infine, il codice binario sarà: "00100111-10100100-10001000".
Se il colore raffigurato nel primo cerchio fosse il colore del primo pixel della nostra immagine, i primi 3 byte (o i primi 24 bit) utilizzati nella memoria informatica per rappresentare l'immagine sarebbero esattamente come sopra scritto, cioè: "001001111010010010001000".
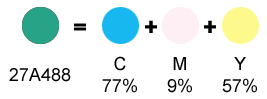
Non dobbiamo confondere la luce che permette alle superfici di riflettere i colori con gli inchiostri colorati che servono per stampare le immagini (per esempio gli inchiostri della stampante).
In questo caso si utilizza la codifica CMY (Cyan, magenta, yellow, cioè ciano, magenta e giallo).
In questo caso il colore finale si ottiene con la sovrapposizione dei tre colori (inchiostri colorati) principali. Utilizzando nessuno dei tre colori avremo il bianco (supponendo che si stampi su carta bianca), utilizzando il massimo della percentuale dei tre colori avremo il nero.
Nella figura si vede lo stesso colore di cui prima abbiamo ottenuto il codice RGB, vediamo che in questo caso, se volessimo stampare quel colore (quello del primo cerchio) dovremmo utilizzare il 77% di colore ciano, il 9% di colore magenta e il 57% di colore giallo sovrapponendoli (e mischiandoli) l'uno sugli altri.
Antonino Fleres